Medidas de dispersão

As medidas de dispersão avaliam a quantidade de diferença entre os dados, ou seja, o quanto estas amostras variam. A medida de dispersão descreve o quão distantes as amostras estão do valor central.

As medidas de dispersão servem também para avaliar qual o grau de representação da média.

A dispersão é importante e demonstra que apenas a média não é o suficiente para descrever um determinado grupo de dados.

Afinal dois grupos podem ter a mesma média mesmo sendo muito diferentes na amplitude em que os dados variam exemplo:

• Grupo 1{6,6,6}
• Grupo 2{18,0,0}
• Grupo 3{8,6,4}

Podemos ver que a média é sempre a mesma, 6. Mas apesar disso há diferenças gritantes entre os 3 conjuntos.

No primeiro não há variação entre os dados e, no segundo há uma variação muito maior que no terceiro.

Deste modo o melhor jeito de apresentar os dados é aplicar uma medida de dispersão além da média. Então, vamos falar dessas medidas? 

Amplitude

A amplitude nada mais é do que a diferença entre o maior e o menor conjunto de dados.

Exemplo: No conjunto ordenado 1,3,5,7,9 a amplitude R seria 9-1 (o maior menos o menor) cujo resultado seria 8.

Para calcularmos o desvio padrão, é necessário calcular a variância a notação que é usada com mais frequência é:

s²=variancia amostral

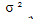
=variancia populacional

s=desvio padráo amostral

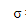
=desvio padrão populacional

Variância populacional

A variância de uma população de “n” elementos é a somatória de cada posição Xi, menos o valor médio do conjunto dividida pelo número de elementos “n”. Segue fórmula:

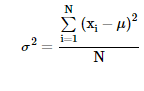
Variância amostral

A variância de uma amostra de “n” elementos é a somatória de cada posição Xi  menos a sua média x dividido pelo número de elementos – 1. Ao utilizarmos a média amostral como estimador de “n” para calcularmos a variância amostral, perdemos 1 grau de liberdade em relação à variância populacional.

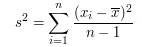
Desvio padrão

Tanto os desvios padrões populacionais quanto os amostrais são calculados tirando a raiz quadrada da variância

Desvio padrão populacional =

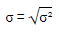
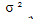
 =variancia populacional

Desvio padrão amostral s=s²

s= Variancia amostral