Distribuição normal: o que é, quando ocorre e exemplos

Se você olha para a renda variável e pensa que é tudo uma questão de sorte, vale repensar.

Mesmo sem uma bola de cristal, existe matemática capaz de ajudar o investidor a estimar a probabilidade de um retorno acontecer — e não apenas “torcer” por ele.

Uma das ferramentas mais usadas para isso é a distribuição normal, e também a sua versão ajustada, a distribuição normal padrão. Elas permitem analisar, por exemplo, com que frequência um retorno tende a ficar em torno da média. Interessante, não é?

Então fica comigo: hoje você vai entender, de forma simples e prática:

• O que é a distribuição normal;
• Como identificar quando uma distribuição é normal;
• Qual é a fórmula da distribuição normal;
• Como usar a função da normal no Excel;
• Quais são as três propriedades da distribuição normal;
• Quais são os principais intervalos da normal.

E claro: exemplos práticos tanto da normal geral quanto da normal padrão. Vamos nessa?

O que é a distribuição normal?

Também chamada de Distribuição Gaussiana, Curva de Gauss ou Curva de Sino, a distribuição normal é um modelo probabilístico usado para descrever como os valores de uma variável aleatória contínua se distribuem.  Ela mostra com que frequência esses valores aparecem em torno da média.

Com essa modelagem, ao conhecermos a média e o desvio-padrão de um conjunto de dados, podemos estimar a probabilidade de observar um determinado valor X dentro de um intervalo definido.

Por sua grande capacidade de representar diversos fenômenos naturais, a distribuição normal é um dos modelos matemáticos mais utilizados em inferência estatística — análises que usam um conjunto pequeno de dados para tirar conclusões sobre um grupo maior.

Isso acontece porque muitos fenômenos naturais apresentam distribuições de probabilidade aproximadamente normais, independentemente de quão aleatórios ou diferentes sejam os valores individuais da amostra.

Assim posto, se a média de altura de um brasileiro é de 1,75m, ao reunirmos 1.000 pessoas aleatoriamente, a maior parte delas terá alturas próximas desse valor, enquanto valores muito abaixo ou muito acima serão cada vez mais raros.

No mercado financeiro — e nas provas de certificação — a distribuição normal costuma ser utilizada para estimar a probabilidade de um retorno se encontrar dentro de um determinado intervalo. Nesse sentido, ela ajuda a medir o nível de confiança (ou incerteza) associado a um resultado.

Quando a distribuição é normal?

Uma distribuição é considerada normal quando os dados formam a clássica “curva de sino”: muitos valores concentrados perto da média e cada vez menos valores à medida que nos afastamos dela. 

Esse padrão fica fácil de ver num histograma, onde a forma curva e simétrica denuncia que os dados seguem — ou se aproximam de — uma distribuição normal, como mostrado abaixo:

Distribuição normal fórmula

A fórmula da distribuição normal é a seguinte:

Onde:

• 𝜇 (mi): média da distribuição, que representa o valor central;
• 𝜎 (sigma): desvio padrão da distribuição, que mostra a dispersão dos valores em torno da média;
• 𝑥: o valor da variável aleatória, que se deseja calcular a probabilidade;
• 𝜋: constante matemática pi (aproximadamente 3,1415);
• 𝑒: base do logaritmo natural (número de Euler, aproximadamente 2,71828).

Para descomplicar dá para dividir essa fórmula em duas partes:

• 1. Fator de escala: ajusta a altura da curva dependendo do desvio-padrão.

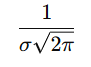
• 2. Termo que controla a forma da curva: quanto mais distante de μ, mais a altura cai.

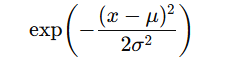
Se fosse traduzir em palavras teríamos algo mais ou menos assim:

altura da curva = constante da escala x e(distância ao quadrado dividida pela variância)

Complicado? Não precisa se preocupar. O Excel está aqui para te ajudar.

Distribuição normal no Excel

No Excel o processo é muito mais simples. Não é preciso escrever a fórmula completa, apenas usar a função pronta.

Para encontrar a densidade da normal (a “altura) curva) use:

• =NORM.DIST(x; média; desvio_padrão; FALSO)

O FALSO indica a função de densidade.

Já para encontrar a probabilidade acumulada use:

• =NORM.DIST(x; média; desvio_padrão; VERDADEIRO)

O VERDADEIRO dá a probabilidade até x.

Exemplo: 

Densidade em x = 180, média 175 e desvio 10:

• =NORM.DIST(180; 175; 10; FALSO)
  • O resultado será a altura da curva normal naquele ponto.

Já a probabilidade de alguém ter menos de 180:

• =NORM.DIST(170; 165; 10; VERDADEIRO)
  • O resultado será a probabilidade de X ser menor ou igual a 180.

Note que o Excel não cria gráficos, curvas ou histogramas sozinho. Essa ferramenta tão somente devolve o valor da função naquele ponto.

Quais são as 3 propriedades da distribuição normal?

As três propriedades clássicas da distribuição normal são:

• 1. Formato de curva de sino: a maior parte dos valores fica concentrada perto da média, e a frequência diminui gradualmente à medida que nos afastamos dela. Em outras palavras, muitos valores no centro, poucos nas extremidades (as “caudas”);
• 2. Simetria em torno da média: a curva normal é perfeitamente simétrica. Média, mediana e moda são iguais e estão localizadas exatamente no centro da distribuição;
• 3. Formato determinado por dois parâmetros: a distribuição normal é completamente definida por:
  • µ (média): indica onde a curva se posiciona no eixo horizontal; em finanças, costuma representar o retorno médio esperado de um ativo ou portfólio.
  • σ (desvio-padrão): indica o “alargamento” da curva, isto é, o quanto os valores se dispersam em torno da média.

Além disso, como a distribuição normal se estende de −∞ a +∞, as caudas da curva vão ficando cada vez mais baixas à medida que se afastam do centro. Elas se aproximam do eixo x, mas nunca chegam a tocá-lo.

Quais os intervalos da distribuição normal?

A curva da distribuição normal normalmente abrange três intervalos de distância em relação ao centro — muitas vezes chamados de Regra 68-95-99,7.

 Estes intervalos mostram como os valores se concentram em torno da média e como a probabilidade diminui à medida que nos afastamos dela:

• ±1 desvio-padrão da média (entre 1,65 m e 1,85 m): cerca de 68% da população;
• ±2 desvios-padrão da média (entre 1,55 m e 1,95 m): cerca de 95% dos valores;
• ±3 desvios-padrão da média (entre 1,45 m e 2,05 m): aproximadamente 99,7% das alturas observadas.

Essas faixas de probabilidade ajudam a entender por que valores muito baixos ou muito altos — como 1,40m ou 2,10m — são tão improváveis: ambos estão além de 3 desvios-padrão da média, numa região onde esses eventos são raríssimos.

Exemplo de distribuição normal

Para facilitar, deixe-me retomar um exemplo que citei anteriormente: a média de altura dos brasileiros, de 1,75 m. 

Se assumirmos um desvio-padrão de 10 cm (0,10 m) — que representa o quanto as alturas variam em torno dessa média —, ao distribuir 1.000 pessoas aleatórias num gráfico, o que aparecerá é justamente a curva de sino (distribuição normal). 

Ao representar isso graficamente, teríamos algo parecido com:

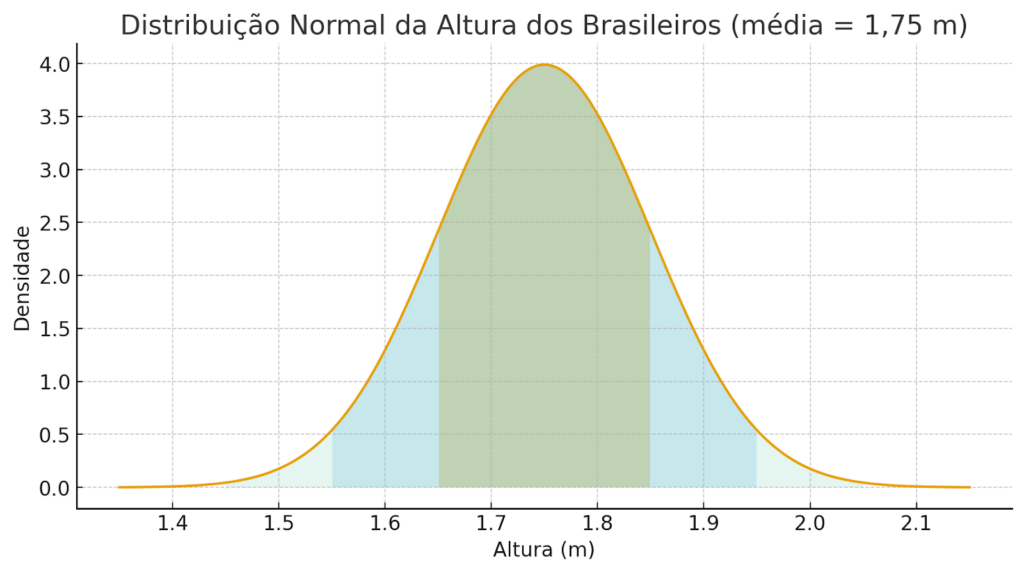
Ao passar os olhos no gráfico, podemos tirar algumas conclusões bastante interessantes:

• Se a média de altura é de 1,75m, a probabilidade de que um indivíduo escolhido ao acaso seja maior ou menor do que esse valor é de 50%;
• A maior parte da amostra ficará concentrada entre 1,65m e 1,85m (±1 desvio-padrão), onde a densidade de valores é maior;
• À medida que nos afastamos dessa faixa — tanto para baixo quanto para cima — a quantidade de pessoas diminui rapidamente;
• A probabilidade de encontrar alguém com 1,40m é tão baixa quanto a de encontrar alguém com 2,10m.

Note que a distribuição normal pode partir de médias (µ) e desvio-padrão (σ) totalmente arbitrários. Nesse caso:

• µ = 1,75m;
• σ = 0,10m;

Agora, como descobrir, por exemplo, qual a probabilidade de uma pessoa com menos de 1,80m aparecer dentro dessa amostragem?

Para isso é preciso  transformar (ou padronizar) esse valor para a escala da normal padrão. Ou seja, levar esse valor X para dentro do desvio normal padrão. Abaixo te ensino a fazer isso.

Distribuição normal padrão

A normal padrão ou normal reduzida é apenas uma versão “ajustada” da distribuição normal comum.  Em vez de ter qualquer média e qualquer desvio-padrão, essa modelagem tem sempre:

• Média = 0;
• Desvio-padrão = 1.

A ideia por trás disso é simples: se todas as distribuições forem trazidas para essa forma padronizada, é possível usar uma única tabela — a famosa tabela da normal padrão, ou tabela Z —  para calcular probabilidades, em vez de ter uma tabela diferente para cada média e desvio-padrão existentes.

Se temos uma variável X com média μ e desvio-padrão σ, podemos transformá-la para a normal padrão usando a seguinte fórmula:

• Z =x – μσ

Esse processo chama-se padronização. Ele converte o valor original (altura, retorno, peso, nota…) em um número que diz quantos desvios-padrão esse valor está acima ou abaixo da média.
O valor resultante dessa padronização é chamado Z-score, que pode ser interpretado da seguinte forma:

• Z = 0 → valor exatamente na média;
• Z = 1 → valor 1 desvio-padrão acima da média;
• Z = –2 → valor 2 desvios-padrão abaixo da média.

Depois de transformar X → Z, é só usar a tabela normal padrão (também chamada tabela Z) para descobrir qual é a probabilidade acumulada até aquele valor Z. Por ser sempre a mesma (média 0, desvio 1, forma fixa), ela funciona para qualquer tipo de variável: alturas, notas, tempos e, claro, retornos financeiros.

Exemplo de distribuição normal padrão

Voltando ao exemplo da altura média do brasileiro, vamos descobrir agora qual é a probabilidade de uma pessoa ter menos de 1,80m (X), se a média é 1,75m e o desvio-padrão 0,10m. Para isso, é só seguir as etapas abaixo:

1. Padronizar o X para Z:

Z =1,80 – 1,750,10 =0,50

Isso significa que a altura de 1,80m está meio desvio-padrão acima da média.

2. Buscar o Z = 0,50 na tabela da normal padrão:
   O valor é de 0,6915.
3. Interpretar:

Portanto, a probabilidade de que uma pessoa escolhida ao acaso tenha menos de 1,80m é de 69%.

Quer aprender mais sobre matemática financeira?

Para ingressar no mercado financeiro ou investir com inteligência, não há como fugir: é preciso entender o mínimo de matemática financeira. Mas não é preciso arrancar os cabelos.

Na TopInvest, traduzimos até os temas mais densos das finanças — como probabilidade e estatística, assunto deste artigo — em uma linguagem que todo mundo entende. Seja qual for a tua dúvida sobre o mercado, temos conteúdo claro, didático e feito para quem quer realmente entender. Explora o nosso blog e o nosso canal no YouTube e continua a aprender com a gente. Até a próxima!